

In particular, Meep supports any material dispersion of the form of a sum of harmonic resonances, plus a term from the frequency-independent electric conductivity: P, in turn, has its own time-evolution equation, and the exact form of this equation determines the frequency-dependence ε(ω). Where (which must be positive) is the instantaneous dielectric function (the infinite-frequency response) and P is the remaining frequency-dependent polarization density in the material. Physically, material dispersion arises because the polarization of the material does not respond instantaneously to an applied field E, and this is essentially the way that it is implemented in FDTD. The actual interface with which you specify these properties is described in the Meep reference. In this section, we describe the form of the equations and material properties that Meep can simulate. Similarly for the relative permeability μ( x), for which dispersion, nonlinearity, and anisotropy are all supported as well.
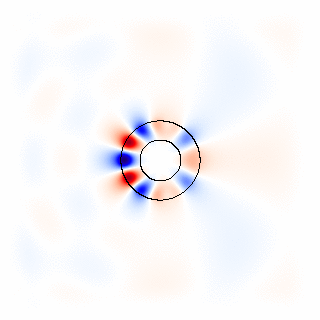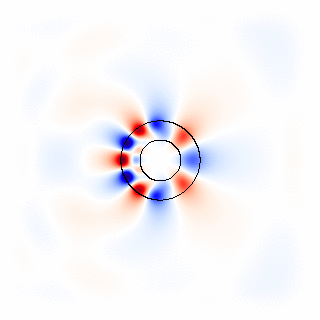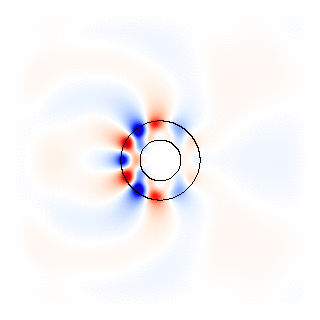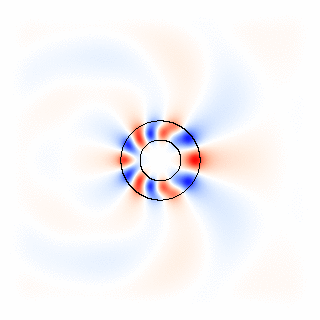
All of these effects can be simulated in Meep, with certain restrictions. Material dispersion, in turn, is generally associated with absorption loss in the material, or possibly gain. It may also depend on the orientation of the field ( anisotropy). In general, it also depends on frequency ( material dispersion) and on the electric field E itself ( nonlinearity). However, ε is not only a function of position. The material structure in Maxwell's equations is determined by the relative permittivity ε( x) and the relative permeability μ( x).


 0 kommentar(er)
0 kommentar(er)
